Famously Isaac Newton and David Gregory disagreed over the maximal number of disjoint unit spheres that can simultaneously touch a central unit sphere. Newton claimed it to be 12, while Gregory thought that a 13-th sphere can fit. It took several centuries to show that Newton was right. Here is your chance to be part of a dispute just like that: make your guess for the double kissing problem.
The kissing number is the maximal number of disjoint (3-dimensional) unit spheres that can touch a common central unit sphere. Today we know the answer is 12. Some optimal solutions have noticable gaps between the outer spheres (see the right figure below) which made people wonder whether a 13-th sphere could fit.
The double kissing problem replaces the central sphere with two spheres:
Given two touching unit spheres, what is the maximal number of disjoint unit spheres that can be arranged so that each touches at least one of the central spheres?
It is not hard to come up with an arrangement of 18 spheres by taking a part of the fcc lattice (or A3 lattice):
As of writing, it seems that a 19-th sphere cannot made fit.
However, in 2015 Moritz Firsching found that by shrinking the outer spheres by a tiny amount, to a radius of not less than 0.99, we actually can fit a 19-th sphere! Here is an animation of this arrangement based on coordinates provided by him on MathOverflow:
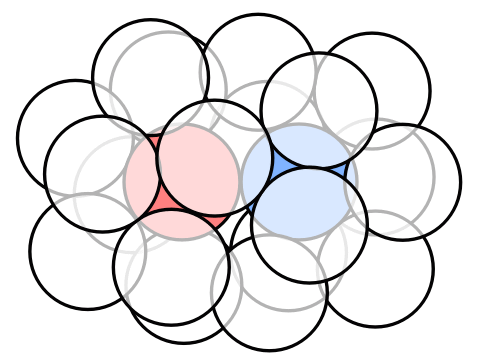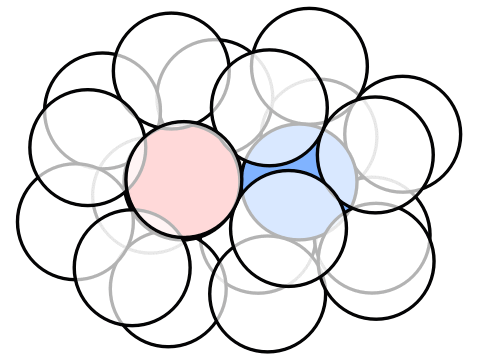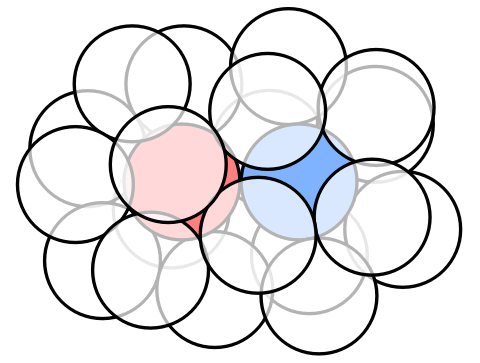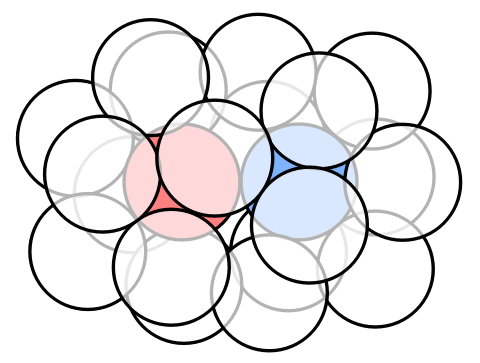
While I am still rooting for double kissing number 18, this 19-sphere arrangement made me pessimistic regarding the existence of a slick argument for this.
The double kissing problem was initially brought to my attention by Florian Theil. In his paper “Face-Centered Cubic Crystallization of Atomistic Configurations” with Lisa Flatley they showed that the fcc lattice is (asymptotically) an energy minimizer for suitably chosen 2- and 3-point potentials. 2-point potentials (that is, the energy depends on the distance between pairs of particles) are familiar from the classical electrostatic and gravitation forces. In contrast, 3-point potentials (the energy depends on the distances in triples of particles) struck me as less natural (though Florian explained to me that they are not unphysical). In fact, Flatley and Theil conjecture that the 3-point potentials are actually not necessary for their result. They can prove this conditional on a new Conjecture 2.2, which reads (in my words):
Conjecture (Flatley, Theil, 2015)
Given a packing of unit sphere in which each sphere touches exactly 12 other spheres, then for any pair of touching spheres there are at least four spheres that touch both of them.
If the double kissing number were 18, then this would answers their conjecture affirmatively: let \(B_0,B_1\) be two touching spheres in an arrangement as in the conjecture, and let \(N_i\) be the set of spheres touching \(B_i\) (excluding \(B_{1-i}\)) then \(|N_i|=11\), \(|N_0\cup N_1|\le 18\), and
\[|N_0\cap N_1| = |N_0|+|N_1|-|N_0\cup N_1| \ge 11+11-18 = 4.\]
Their Conjecture 2.2 makes much stronger assumptions than the general double kissing problem and might therefore be more accessible. Note that in the animation of the 19-spheres configuration, there is not a single sphere that touches both central spheres. This is possible since the central spheres are not touched by 12 spheres each, but by 11 and 10 other spheres respectively (including the other central sphere).